Objectif
Réaliser avec python et la bibliothèque turtle sous Thonny des graphiques du style du dessous. L'idée est de s'amuser, de tester puis de comprendre le fonctionnement du script final. Les principes de programmation utilisés sont:
- l'affectation des variables
- quelques commandes de la bibliothèque turtle
- l'utilisation d'un dictionnaire
- la boucle for
- la division entière (modulo)
Pour le principe de fonctionnement de cette table de multiplication d'un nouveau genre partant de turtle et pointant vers Mandelbrot,
voir cette vidéo (de Burkard Polster)
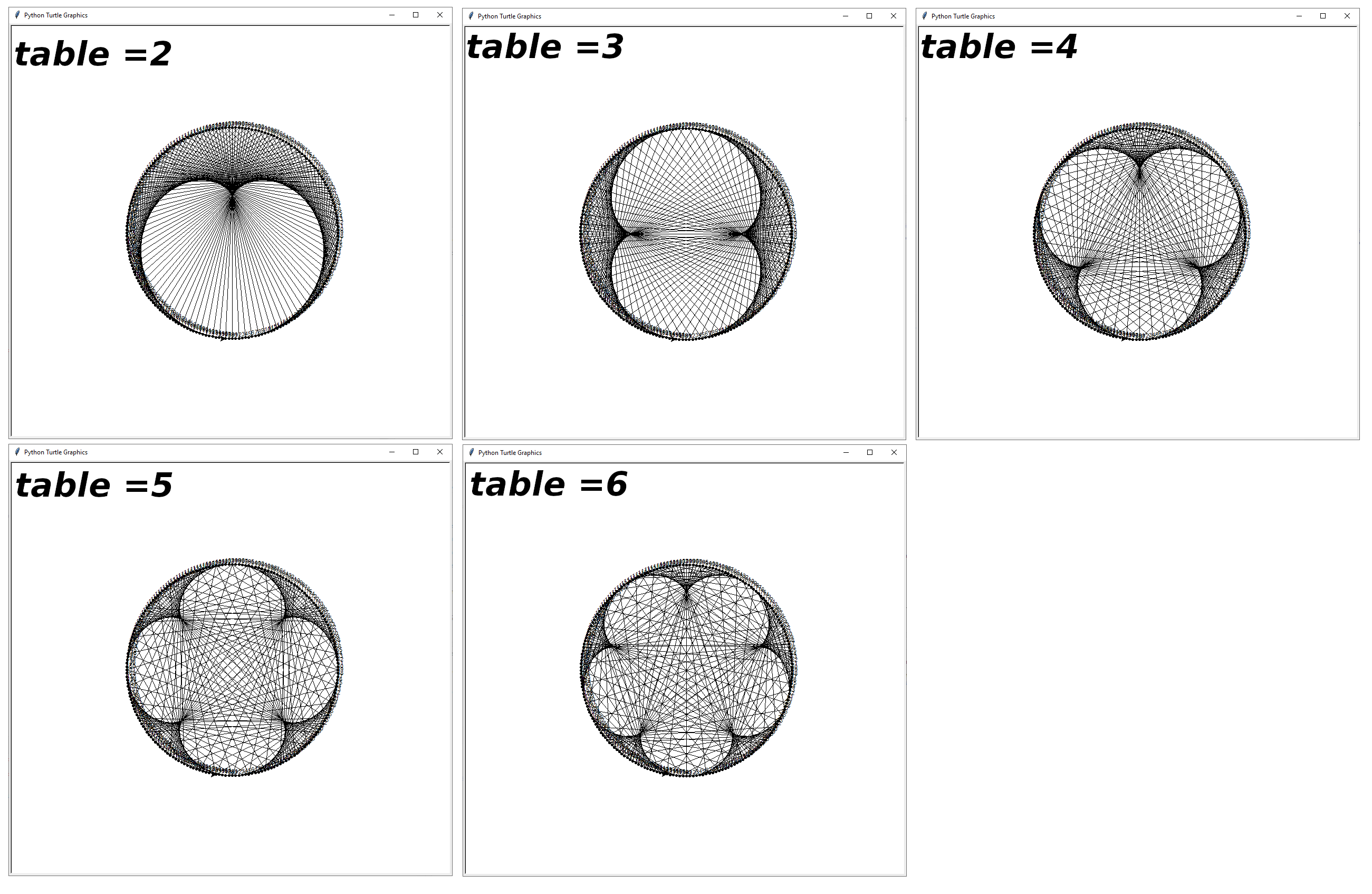
Documentation
Tous les scripts suivants utilisent essentiellement la bibliothèque turtle nativement présente dans python donc tous les scripts commenceront par "from turtle import*".
En dessous quelques liens vers une documentation de Laurent Pointal mise à disposition sur son site https://perso.limsi.fr/pointal/python:abrege.
- Turtle - Aide mémoire de Laurent Pointal
https://perso.limsi.fr/pointal/_media/python:turtle:turtleref.pdf - Python - Mémento de Laurent Pointal
https://perso.limsi.fr/pointal/_media/python:cours:mementopython3.pdf
Les étapes constructivistes du script ultime
Création d'un cercle avec Turtle
Objectif
Tracer un cercle centré dans la fenêtre turtle. Nécessite au début du script un décalage verticalement vers le bas de la longueur du rayon.
Script
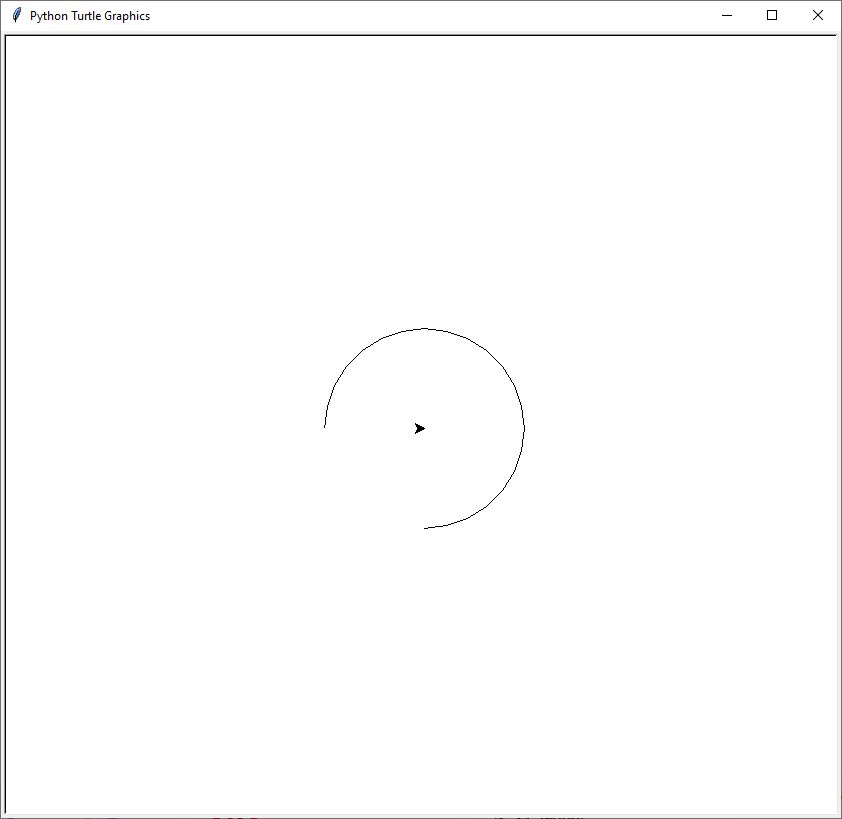
from turtle import *
penup()
goto(0,-100)
pendown()
circle(100,270)
penup()
home()Analyse
- penup() => lève le crayon (pas de trace)
- goto(x,y) => se déplace vers x,y
- pendown() => baisse le crayon (trace)
- circle(rayon, angle) => dessine un cercle
- home() => Retour au point 0,0 de la tortue
Ici je descends de 100 pt sur l'axe des y vers le bas sans tracer de ligne puis je trace un cercle de rayon 100 et d'angle 270°. J'en conclue que je pourrai faire des fragments d'arc de cercle de n parties sur 360°.
Découpage du cercle en x arcs de cercle
Objectif
Découper un cercle en x parties égales. npt représente le nombre de points, ici je prends 11 parties. Comme la logique de découpe est reproductible j'ai l'idée d'utiliser la boucle bornée for ;)!
Script
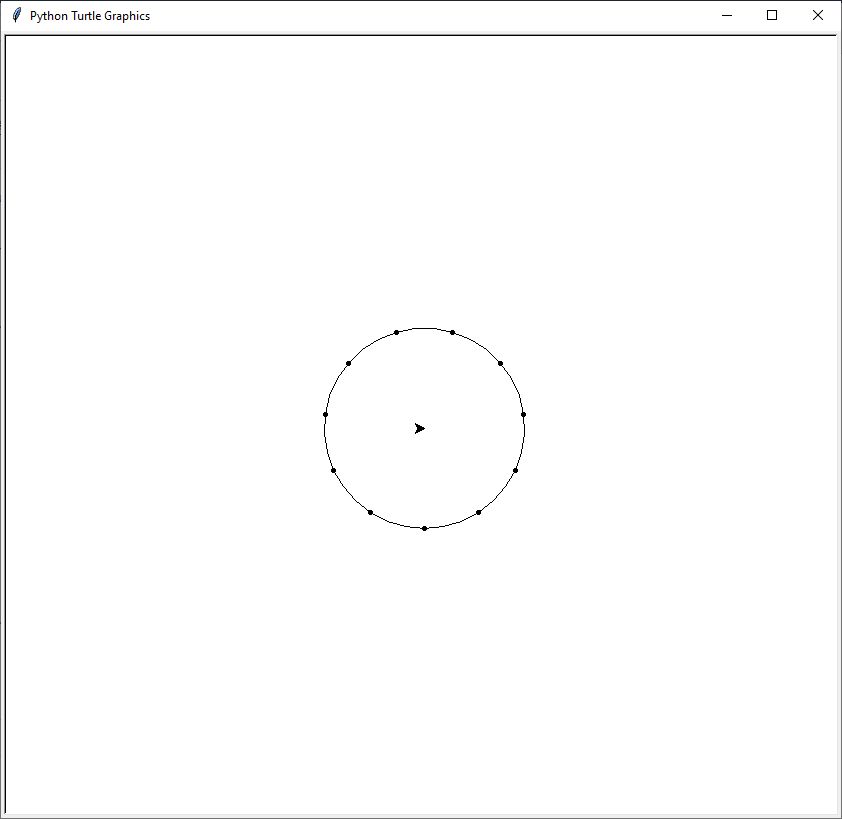
from turtle import *
npt=11
penup()
goto(0,-100)
pendown()
for i in range(npt):
dot()
print(position())
circle(100,360/npt)
penup()
home()Analyse
- ntp => nombre de points = nombre de fragments d'arc = 11 dans cet exemple
- for i in range (npt) => création de npt entier allant de 0 à 10 (npt-1=11-1=10)
- dot() => crée un point à la position de la tortue
- position() => relève les coordonnées (x,y) de la position de la tortue
- print() => affiche dans shell => utile pour voir ce que donne la commande position()
- circle(100,360/npt) => crée un arc de cercle de rayon 100 et de longueur d'arc 360/11 ième dans cet exemple
(si vous utilisez le mode débug de Thonny, vous noterez que circle crée des arcs de 32.72° en partant du dernier point placé - ce qui est cool)
Je dispose de la base qui me permettra de construire la suite du script car je visualise les segments d'arc et j'ai les coordonnées des points. Je veux maintenant afficher les n° des points de 0 à 11 sur le cercle et surtout je veux enregistrer les coordonnées quelque part. Pour l'enregistrement je pense soit à une liste, soit à un dictionnaire (je pense que les deux fonctionneront!)
A ce niveau de maîtrise, si je vous êtes curieux vous pouvez aller voir:
et retourner un peu en enfance ;)
Affichage des n° des points sur le cercle et ajout de la liste dans un dictionnaire
Objectif
Afficher près de chaque point son label (son n° de 0 à npt-1) et enregistrer les coodonnées des points dans un dictionnaire. L'intérêt du dictionnaire est de pouvoir par la suite appelé les coordonnées d'un point en utilisant son nom ou label ;).
Je veux aussi pouvoir jouer avec le rayon du cercle pour modifier si besoin sa taille afin de mieux voir les noms des points si besoin.
Script
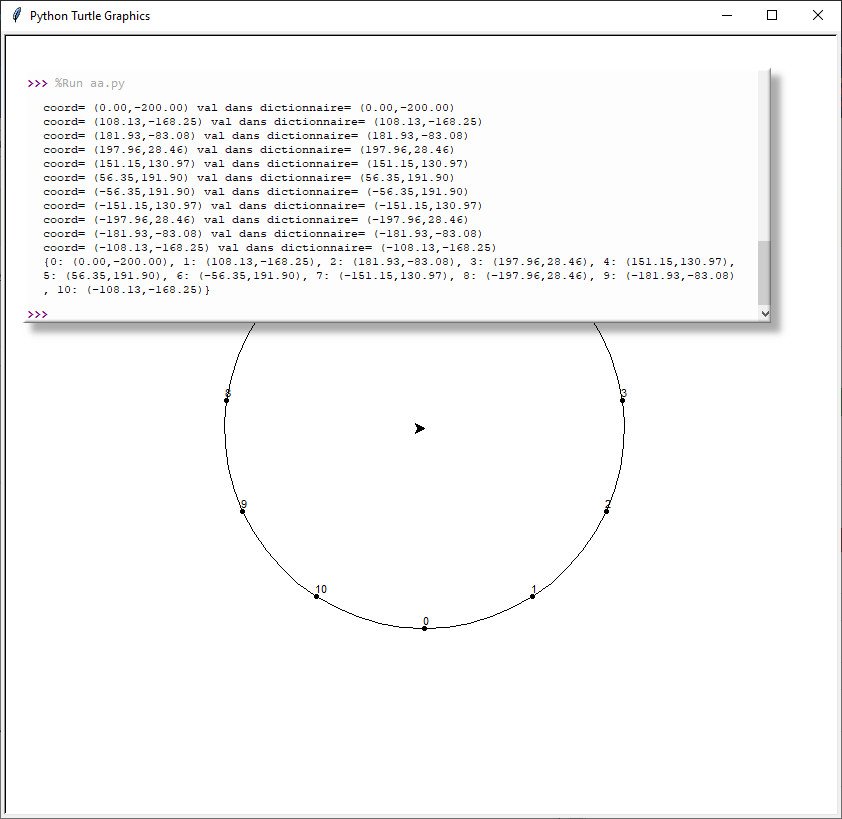
from turtle import *
rayon=200 #rayon du cercle
npt=11 #nbre de points
pos={} #dictionnaire
penup()
goto(0,-rayon)
pendown()
for i in range(npt):
dot()
write(i)
pos[i]=position()
print("coord=",position(),"val dans dictionnaire=",pos[i])# pour comprendre
circle(rayon,360/npt)
print(pos)# pour visualiser le dictionnaire label:(valeurs)
penup()
home()Analyse
- # symbole me permettant d'ajouter dans mon script des commentaires
- variable rayon=200 => pour pouvoir modifier le rayon de mon cercle => donc je dois remplacer la valeur 100 dans mon goto et dans circle par la variable rayon
(vous noterez le commentaire) - pos={} => création d'un dictionnaire se nommant "pos". Comme entre les accolades il n'y a rien, mon dictionnaire est vide
- goto(0,-rayon) => remplace maintenant le goto(0,-100) car le décalage vers le bas doit rester cohérent avec ma valeur de rayon
- write(i) => commande qui écrit la valeur de i dans turtle à l'endroit où se trouve la tortue - ce qui tombe bien après le dot()
- pos[i]=position() => affectation des coordonnées (position()) dans le dictionnaire
pos[0] = (0.00,-200.00)
pos[1] = (108.13,-168.25)
... - print("coord=",position(),"val dans dictionnaire=",pos[i]) => donne l'affichage suivant dans le shell
coord= (0.00,-200.00) val dans dictionnaire= (0.00,-200.00)
...
coord= (-108.13,-168.25) val dans dictionnaire= (-108.13,-168.25)
Je comprends donc que le dictionnaire pos contient les entrées i=0, i=1... et que je peux appeler chaque coordonnées avec pos[i] - print(pos) => n'est plus dans la boucle for donc affichage final du dictionnaire
{0: (0.00,-200.00), 1: (108.13,-168.25), 2: (181.93,-83.08), 3: (197.96,28.46), 4: (151.15,130.97), 5: (56.35,191.90), 6: (-56.35,191.90), 7: (-151.15,130.97), 8: (-197.96,28.46), 9: (-181.93,-83.08), 10: (-108.13,-168.25)}
soit { label 0 : valeur associée au label 0 , label 1 : valeur associée au label 1 , ... , label final : valeur associée au label final }
Le plus dur me semble fait, je dispose des coordonnées, je peux appeler les coordonnées, et à l'aide d'un pendown() et de goto(x,y) je dois bien pouvoir faire un trait entre deux points.
Création d'un trait entre deux coordonnées arbitrairement choisies i et j
Objectif
Tout est dans le titre... Et je constate que le monde est bien fait ;)))
Script
from turtle import *
rayon=200 #rayon du cercle
npt=11 #nbre de points
pos={} #dictionnaire
penup()
goto(0,-rayon)
pendown()
for i in range(npt):
dot()
write(i)
pos[i]=position()
circle(rayon,360/npt)
penup()
home()
# tracer des traits
goto(pos[2])
pendown()
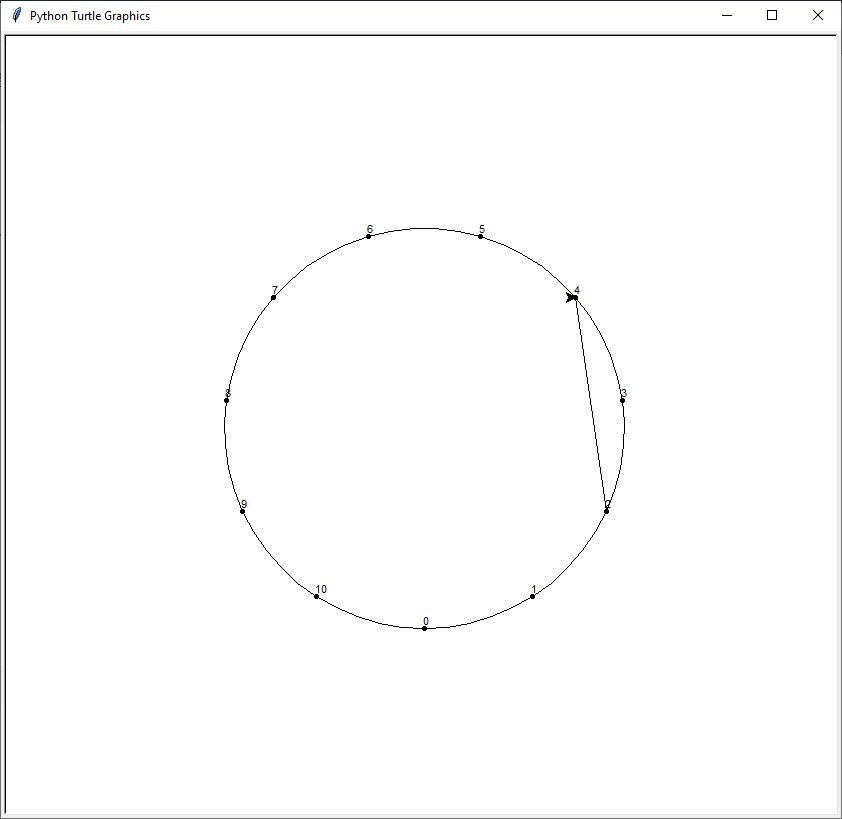
goto(pos[4])Analyse
- notez le penup () après la boucle
- goto(pos[2]) => goto((181.93,-83.08)) = goto (181.93,-83.08) = goto ( x , y) dans l'exemple du dessus
puisque penup() avant le commentaire #tracer la tortue va se déplacer à la position 2
puis - pendown() => le stylo trace
- goto(pos[4]) => je trace donc un trait de la position 2 à la position 4
L'idée maintenant est d'insérer dans la boucle ce principe de traçage de traits. Je dois relier le point i au point j qui est le double de i si je travaille avec la table de 2. Si vous ne comprenez pas, je vous conseille de revoir la vidéo suivante: https://youtu.be/qhbuKbxJsk8
En approche de le script ultime - boucle et tracer des traits
Objectif
Insérer dans une boucle le tracé des traits en appliquant le principe pour la table de 2. Mais je veux faire tous les jolis dessins de Burkard Polster - Je pense alors variable ;)
Script
from turtle import *
rayon=200 #rayon du cercle
npt=10 #nbre de points
table=2 #variable pour la table de multiplication
pos={} #dictionnaire
penup()
goto(0,-rayon)
pendown()
for i in range(npt):
dot()
write(i)
pos[i]=position()
circle(rayon,360/npt)
penup()
home()
print(pos) #pour comprendre
# tracer des traits
for i in range (npt):
penup()
j=i*table
goto(pos[i])
pendown()
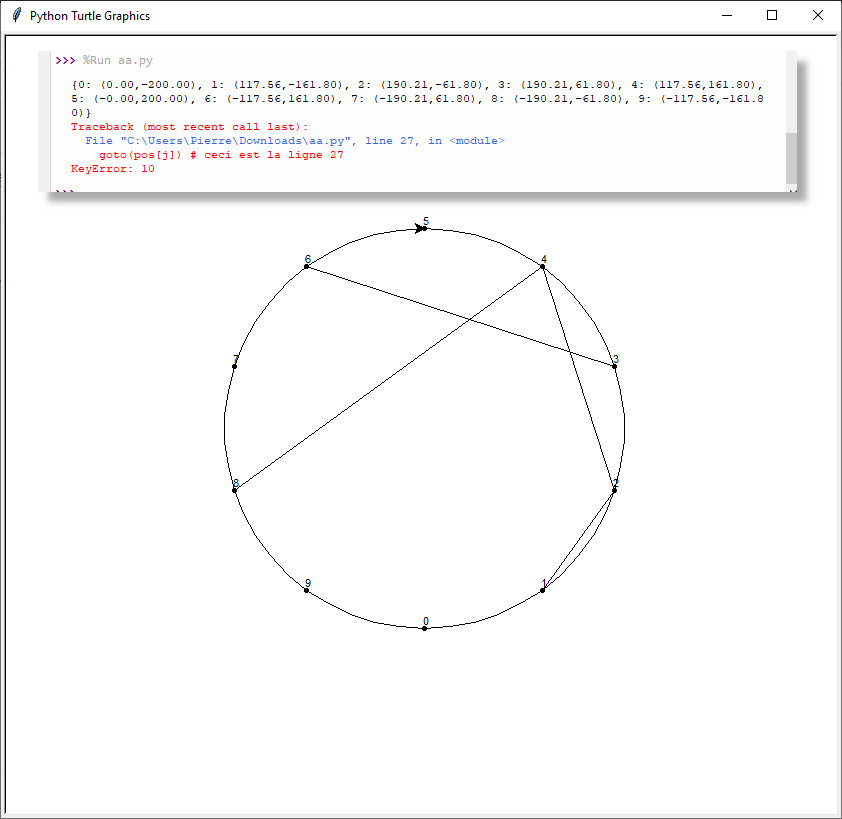
goto(pos[j]) # ceci est la ligne 27Analyse
- table=2 => valeur de la table arbitrairement choisie, je déclare une variable car vous vous doutez bien que je veux faire des dessins avec 2, 25, 51...
En fin de script
- # tracer des traits => commentaire début du tracé
- for i in ... => je boucle de 0 à 10 dans le cas présent => donc j'envisage 10 traits
- j=i*table => calcul la valeur de mon point d'arrivé pour la table de 2 dans le cas présent
et je me doute que je ne traite pas les valeurs finales du genre si i=10 alors j=10*2=20 et je n'ai pas dans mon dictionnaire l'entrée 20:
Je comprends le message d'erreur dans le shell... je n'ai que 10 entrées dans mon dictionnaire pour des i allant de 0 à 9 donc évidement que cela coince pour j quand i=5. Je dis i=5 car ma tortue est bloquée dans mon dessin sur cette valeur ;)
Script ultime - le graal
Objectif
Pouvoir dormir ce soir ;) et vous proposer, j'en suis assez fier, un script qui fonctionne dans tous les cas de figure...
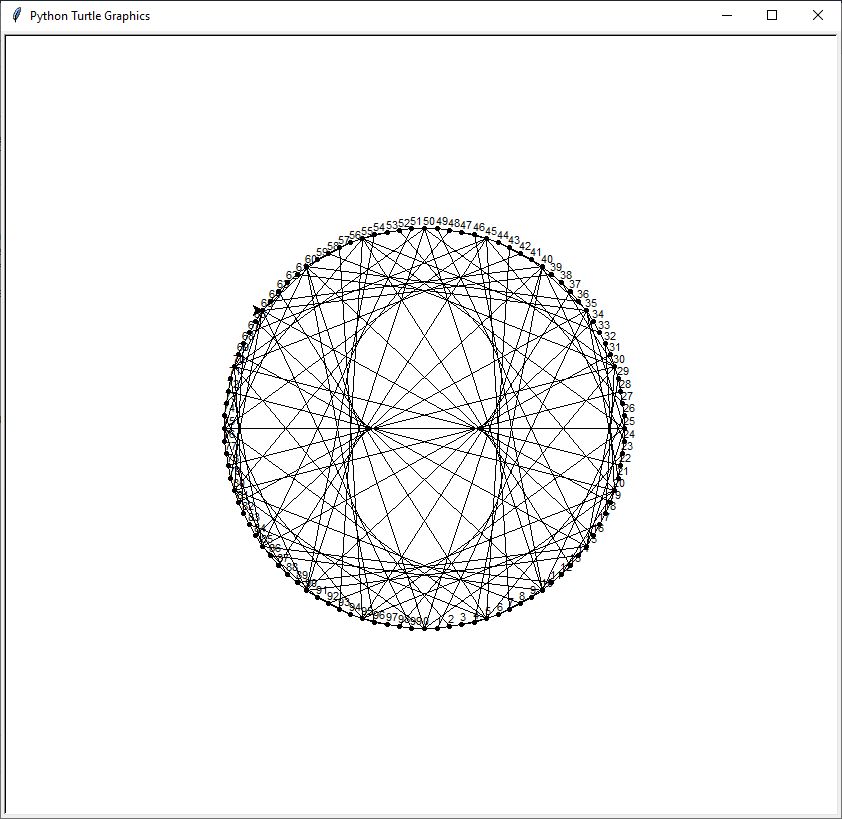
Pour vous impressionner avec un joli dessin, vous noterez les valeurs utilisées dans la fenêtre Python Turtle Graphics:
- rayon=200 #rayon du cercle
- npt=100 #nbre de points
- table=35 #Saisir ici des valeurs entières
Script
from turtle import *
# jouer avec les valeurs npt et table
# si dessin pas à la bonne taille jouer alors avec rayon
rayon=200 #rayon du cercle
npt=100 #nbre de points
table=35 #Saisir ici des valeurs entières
# la suite n'est pas à modifier!!
pos={} #dictionnaire
penup()
goto(0,-rayon)
pendown()
for i in range(npt):
dot()
write(i)
pos[i]=position()
circle(rayon,360/npt)
penup()
home()
# tracer des traits
for i in range (npt):
penup()
j=i*table
goto(pos[i])
pendown()
goto(pos[j%npt]) # voir l'analyse pour comprendre ce moduloAnalyse
En vidéo avec Thonny et le mode débug. L'idée est de résoudre le problème de l'étape précédente pour des j supérieurs au nombre de points de mon cercle. La discussion tourne donc autour de la dernière ligne:
goto(pos[j%npt]) # voir l'analyse pour comprendre ce modulo
- j%npt => donne le reste de la division entière de j par npt ce qui correspond au modulo en mathématique
https://www.youtube.com/watch?v=cvP_QffIqXI